前言：为了整活好玩的东西，没有数学功底和深度学习经验的萌新开始学 NLP 了！
看的课程链接是这个：https://www.deeplearning.ai/natural-language-processing-specialization/
然后呢，大概会不定期更新一下学的过程中记下来的一些东西。顺便安利一下 Notion 这个笔记软件，实在是太好用啦。

Sentiment analysis 情感分析

任务：预测一个语句带有正面情绪 (positive, 1) 或负面情绪 (negative, 0)。

Vocabulary 词汇表

假设你有一个语句的集合 $S$，那么词汇表 (vocabulary) $V$ 包含了 $S$ 中的每个独立的单词。

示例：

$$V = {I, am, happy, because, learning, NLP, …, hated, the, movie}$$

Feature extraction 特征提取

方法一：稀疏表示 Sparse Representation

将一个句子 (tweet) 表征成一个向量 (vector). 例如，将一个句子中所出现的所有词汇，使用一个长度为 $|V|$ 的向量 $\vec{v}$ 表示；$\textbf{v}_i$ 为词汇表 $V$ 中第 $i$ 个元素的出现次数。

使用上述方法表征句子的特征时，向量 $\vec{v}$ 中会有大量的 0 元素，是一个 稀疏表示 (sparse representation)。

稀疏表示带来了一些问题，如果使用此方法表示特征，则线性回归模型需要学习 $n+1$ 个参数 $\theta_0, \theta_1, …, \theta_n$ （$n = |V|$）；当词汇表的数量 $|V|$ 很大时，将会产生更长的训练时间和更长的预测时间。

方法二：生成计数 Generate Count

假设标签分为两类：positive 和 negative.

定义词汇表中每个单词具有两个属性： PosFreq 和 NegFreq，分别表示该单词在所有表达正面情绪的句子中出现的次数，和在负面情绪的句子中出现的次数。简而言之，

$$freqs = (word, class) ⇒ frequency.$$

接下来，将一个句子表征成一个具有 $c+1$ 个维度的向量（$c$ 是分类的数量）。此时，线性回归模型不需要学习 $|V|$ 个特征，而只需要学习 $3$ 个特征。对于任意的句子 $m$，它的特征向量 $X_m$ 可以表示为：

$$X_m = [1, \sum_w freqs(w,1), \sum_w freqs(w, 0)]$$

解释一下上面这个向量表示，其中：

• 第一维元素 1 表示 偏置(bias)
• 第二维元素 $\sum_w freqs(w, 1)$ 表示词汇表中的每个词汇 $w$ 在正面情绪 (label=1) 的句子集合中出现的次数之和
• 第三维元素 $\sum_w freqs(w, 0)$ 表示词汇表中的每个词汇 $w$ 在负面情绪 (label=0) 的句子集合中出现的次数之和

Preprocessing 预处理

1. 删除停顿词和标点符号

为了删除所有的停顿词（如 and, is, are, at …）和标点符号，需要有两个含有停顿词和标点符号的词汇。

但需要注意的是，有些时候并不一定需要删除标点符号，因为有些时候标点符号会为特定的 NLP 任务提供重要信息（如可能改变语义）。

2. 提取词干、转变为小写

提取词干 （Stemming）：通俗地说就是将各种不同形式的词汇转化为原型，例如 tune, tuning, tuned，提取词干后会变成 tun. 提取词干后会使得词汇表中所包含的词汇减少。

为了减少词汇表中的单词数量，需要将词汇转变为小写。

Generate Feature Matrix 生成特征矩阵

假设语料库中有 $m$ 个句子，对所有的句子执行上述预处理操作，并将其表示为一个三维特征向量，最终会得到一个 $m \times 3$ 的 $X$ 矩阵。大体过程如下：

freqs = build_freqs(tweets, labels)    # build frequencies dictionary
X = np.zeros((m, 3))
for i in range(m):
		p_tweet = process_tweet(tweet[i])
    X[i,:] = extract_features(p_tweet, freqs)

Logistic Regression 逻辑回归

逻辑回归的过程示意图：

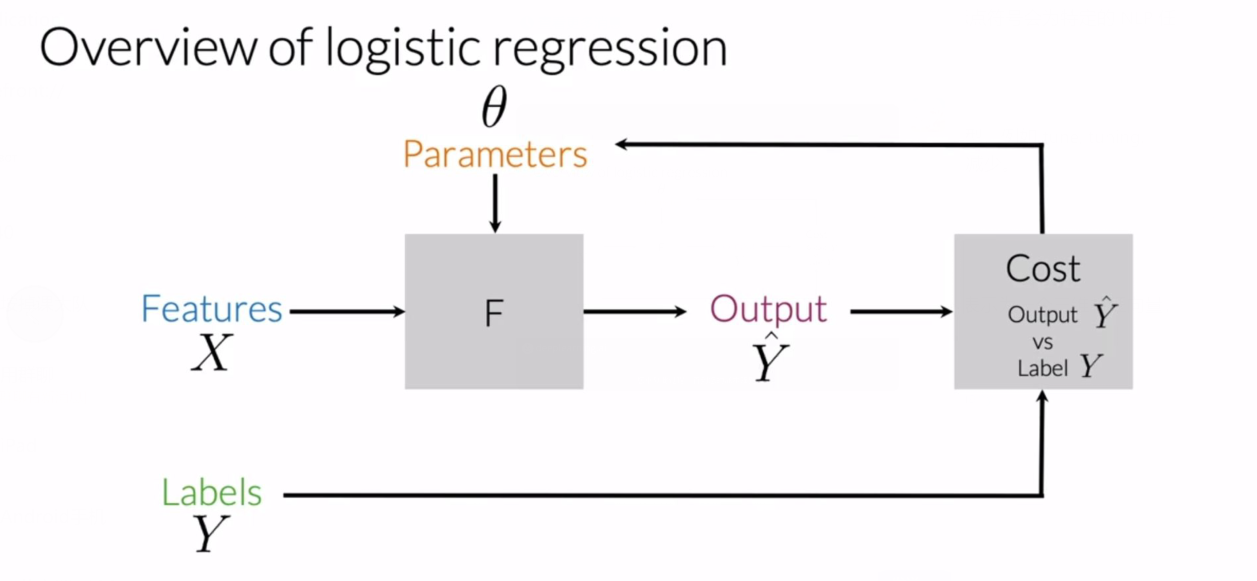
函数 $F$ 是一个 $sigmoid$ 函数 （S 形生长曲线，将变量映射到 $[0, 1]$ 之间）：

$$h(x^{(i)}, \theta) = \frac{1}{1 + e^{-\theta ^T x^{(i)}}}$$

其中 $\theta ^T x^{(i)}$ 是参数列向量 $\theta$ 转置后与第 $i$ 个句子的特征向量 $x^{(i)}$ 的乘积。

一般认为阈值为 0.5。

Training Logistic Regression Classifier 训练分类器

任务：不断迭代寻找使得代价函数最小的参数 $\theta_i$ 。

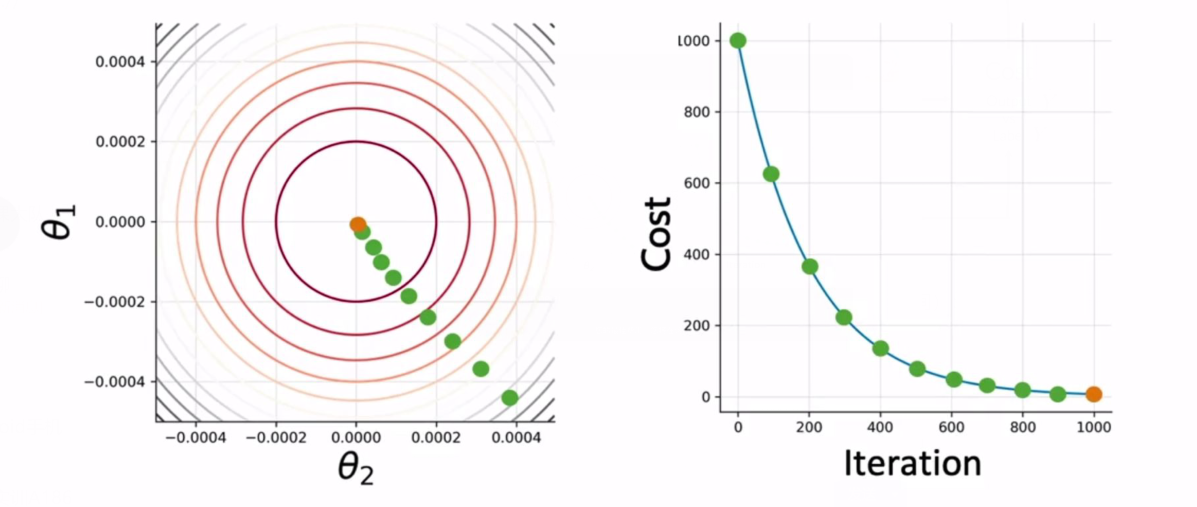
左图为 $\theta_1, \theta_2$ 的不同取值下，代价函数的等高线（越靠近中心点，代价函数越小）；

• 首先取 $\theta_i$ 在任意一个点开始，得到 $h = h(X, \theta)$
• 然后计算 $\theta_1, \theta_2$ 在该点的梯度 $\nabla = \frac{1}{m} X^T (h-y)$
• 使用梯度更新参数 $\theta = \theta-\nabla$
• 然后计算 loss （损失）函数 $J(\theta)$，重复上述步骤直到 $J(\theta)$ 足够好。

上述算法称为梯度下降法（收敛性证明可以看吴恩达的机器学习教程）。右图表示随着迭代次数增加，代价函数 Cost 将降低，且下降速度与梯度有关。

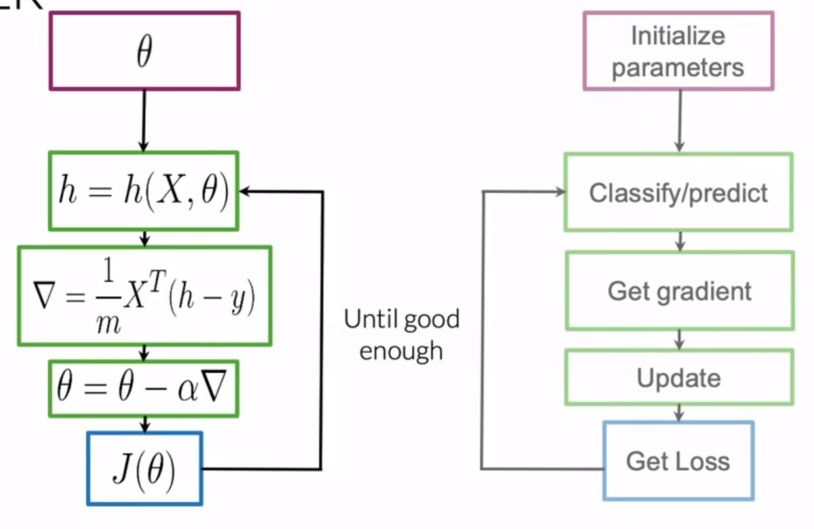
Testing Logistic Regression 测试逻辑回归

验证集 (validate)：$X{val}, Y{val}, \theta$

• 首先计算参数为 $\theta$、自变量为 $X_{val}$ 的 $sigmoid$ 函数
• 计算 $pred = (h(X_{val}, \theta) \ge 0.5)$，0.5 为阈值
• 对比 $pred$ 和 $Y{val}$ ，计算准确率 (accuracy) = $\sum{i=1}^{|val|} \frac{(pred^i == y_{val}^{i})}{m}$

Cost Function 代价函数

代价函数可以表示为以下形式：

$$J(\theta) = -\frac{1}{m} \sum_{i=1}^m [y^{(i)} \log h(x^{(i)}, \theta) + (1 - y^{(i)}) \log (1 - h(x^{(i)}, \theta))]$$

其中 $m$ 是训练集中的句子个数 （size）。

可以看出代价函数 $J(\theta)$ 是对训练集中所有的句子计算某一个值，然后取平均值。负号的作用是让代价函数始终取非负数。

$y$ 的取值可能是 0 或 1，考虑第一项对代价函数的贡献：

• 如果 $y^{(i)}$ 为 0，那么第一项无论 $h$ 取何值都为 0；
• 如果 $y^{(i)}$ 为 1，且 $h$ 接近于 1，则第一项会趋近于 0；
• 如果 $y^{(i)}$ 为 1，且 $h$ 接近于 0，则第一项中的对数会趋于 $-\infty$，从而使得第一项趋于 $-\infty$.

再考虑第二项对代价函数的贡献：

• 如果 $y^{(i)}$ 为 1，则 $1-y^{(i)}$ 为 0，那么第二项无论 $h$ 取何值都为 0；
• 如果 $y^{(i)}$ 为 0，且 $h$ 接近于 0，则第二项会趋近于 0；
• 如果 $y^{(i)}$ 为 0，且 $h$ 接近于 1，则第二项中的对数会趋于 $-\infty$，从而使得第二项趋于 $-\infty$.