这件事要从上一节的信号与系统实验课说起。在老师把连续函数卷积的内容讲完布置作业的时候,他给我们整了一个好活……
“除了上面这些作业之外,要求大家额外做一个附加题,来实现两个函数图解法求卷积动画演示。”
差不多像这样子($f_1(t) = u(t) - u(t-2), f_2(t) = u(t-1) - u(t-3), f_1 * f_2$):
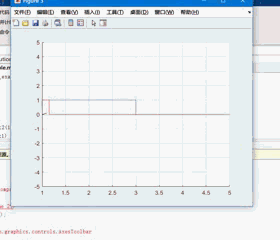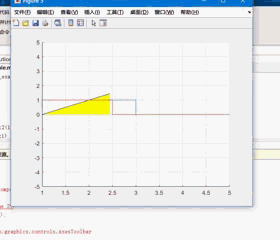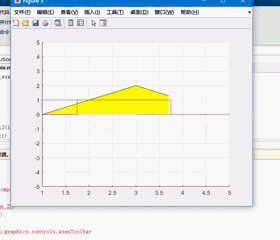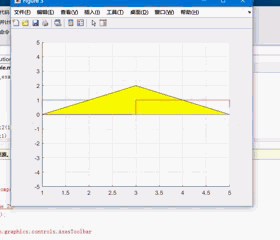
然而我们既不知道这东西具体如何实现,也并没有学过怎么用 MATLAB 做动画,那咋办嘛。
老师:“我希望每个人都要做这个附加题,有 问 题 自 己 去 解 决。”
反正当时我的表情是这样的:

好呗,既然整了这么个好活,那我们就来看看这东西到底咋搞咯。
前置知识
图解法求卷积
定义:函数 $f_1(t)$ 和 $f_2(t)$ 的卷积 $f_1(t) * f_2(t) = \int _{-\infty}^{\infty} f_1(\tau)f_2(t-\tau) d\tau$.
为了求解 $f_1(t) * f_2(t)$,我们可以使用图解法,将卷积运算中一些抽象的关系形象化。具体有以下几个步骤:
- 换元:将横坐标变元由 $t$ 变换为 $\tau$:$f_1(t) \to f_1(\tau)$,$f_2(t) \to f_2(\tau)$
- 固定其中一个信号(如 $f_2(\tau)$),对另一个信号关于纵轴反折:$f_1(\tau) \to f_1(-\tau)$
- 位移:将反折后的信号做位移,位移量是 $t$:$f_1(-\tau) \to f_1(t-\tau)$。首先将 $f_1$ 左移到与 $f_2$ 不重合的位置
- 增大 $t$,将 $f_1$ 向右移动,使得 $f_1(t-\tau)$ 和 $f_2(\tau)$ 发生重叠,将两信号重叠的部分相乘:$f_1(t-\tau)f_2(\tau)$
- 积分:两个信号在该点重叠部分的面积 $\int _{-\infty} ^{\infty}f_1(t-\tau)f_2(\tau) d\tau$ 即为 $f_1 * f_2$ 在点 $t$ 处的函数值
MATLAB 创建动画
所谓动画,就是很多张静态图片,以一定帧数播放而产生的动态效果。
而在 MATLAB 里创建动画的基本原理,也是将使用 plot 等函数绘出来的结果一张张地保存,然后一帧帧地播放,就能产生动态的动画。MATLAB 对此功能的实现提供了一些关键函数,如 getframe, movie 等。
当然,也可以在循环绘图的时候直接指定短暂的停留时间,以此产生动画。可以使用 pause 函数产生短暂的停留。
思路分析
大概有人会说,这不是按照上面图解法的步骤一步一步来就好了嘛。

这样吧,我们最终的目的是要弄出一个动画对吧,这个动画呢它是一帧帧、一张张图组成的,那我们先绘出所有时刻的图吧。
那绘出所有时刻的图,跟画某个时刻的图的区别就在于,其中一个函数会从左到右逐渐平移咯。
对于 $f_1(t-\tau)$ 而言,从左到右平移就相当于将 $t$ 逐渐由小增大。那么我们要实现平移的效果,只要让 $t$ 缓慢、线性地从一个小值 $from$ 变到一个大值 $end$ 就可以了。
然后我们对每个 $t_0$ 值都画一幅 $f_1(t_0-\tau)$ 的图,并且计算 $f_{13}(t) = f_1(t_0-\tau) \cdot f_2(\tau)$ 在 $(-\infty, \infty)$ 的积分值 $f_{14}$,
将 $f_{14}$ 与 $t$ 对应起来,绘在图上就可以了。
两个函数 $f_1, f_2$ 的表示,我们可以用 MATLAB 的符号计算功能,这样我们可以让我们的代码对所有的函数都适用而不需要计算各种向量,并且我们在实现换元、反折和平移的时候也很容易,只要使用 subs() 函数替换自变量即可。
至于符号计算的绘图,那当然是 ezplot 就解决啦……什么?ezplot 是不推荐的函数了?那就用 fplot 呗.
然后把每张图存起来,或者在画连续的两张图的时候有一个小小的时间间隔,就可以了做出动画的效果啦。
实现
让我们首先定义一下我们要卷积的函数。假设我们有了两个函数 $f_1(t) = u(t) - u(t-2), f_2(t) = u(t-1) - u(t-3)$,要用图解法求 $f_1 * f_2$.
% 定义符号变量 t 和两个符号函数 f1, f2
% heaviside(t) 就是 u(t) 啦
syms t;
f1 = heaviside(t) - heaviside(t-2);
f2 = heaviside(t-1) - heaviside(t-3);
d = 0.05; % 采样间隔
t1 = 0 : d : 2; % f1 的卷积时域范围
t2 = 1 : d : 3; % f2 的卷积时域范围
为了让我们写的东西具有普遍适用性,我们将它封装成一个如下的函数:
function [] = convolution_example(f1, f2, t1, t2, d)
函数的参数与上文定义的含义相同。具体函数实现如下:
function [] = convolution_example(f1, f2, t1, t2, d)
syms t tao; % 定义用于符号计算的变量
figure; % 在一个新的窗体上执行绘图
grid on;
hold on; % 因为要多用多次 plot 和 fplot,所以要打开 hold
% 以下计算,可参照连续信号的卷积函数
time_start = t1(1) + t2(1); % 计算卷积结果序列非 0 值的起始位置
time_length = length(t1) + length(t2) - 2; % 计算卷积结果序列非 0 值得宽度
f = time_start; % 时域起始位置 from
e = time_start + time_length * d; % 时域终止位置 end
ymin = -5;
ymax = 5;
f11 = subs(f1, t, t - tao); % 对 f1 进行换元、反折和位移:f1(t) => f1(tau) => f1(-tau) => f1(t-tau)
fplot(f2, [f, e]); % f2 是固定的,可以先画到图上
vec = f : d : e; % 生成卷积结果的时域向量
p1 = fplot(f2, [f, e]); % 定义 p1 绘图句柄
dt = [0]; ft = [0];
% 循环绘图动画,对于卷积结果的时域向量中的每一个 t,都绘制一张该时刻的图
for i = 1 : 1 : length(vec)
f12 = subs(f11, {t tao}, {vec(i) t}); % 令 t0 = vec(i),此时 f12 = f1(t0-tau),即位移量为 t0
f13 = f12 * f2; % 计算位移 t0 后的 f1 与 f2 的相乘结果
delete(p1); % 先删除上一个 f12 的图像
p1 = fplot(f12, [f e]); % 绘制新的 f12
axis([f, e, ymin, ymax]);
set(p1, 'Color', 'r');
f14 = int(f13, f, e); % 计算积分值,即为在 t 时刻的 f1*f2 值
% 为了使得绘出的图像平滑,将当前的 (t, f14) 添加到数组(向量)中,然后调用 plot 就可以绘出光滑的曲线
% 否则,只调用 plot(t, f14) 只能绘出散点图
% 并且,填充曲线下方到 x 轴的区域。根据简单的几何知识,因为间隔 d 足够小,所以只要填充一个梯形即可
% 设当前的 t 值为 v(i),当前函数值为 f(i),那么只要填充梯形 (v(i), f(i)), (v(i), 0), (v(i-1), 0), (v(i-1), f(i-1)) 即可
p2 = fill([dt(length(dt)), dt(length(dt)), vec(i), vec(i)], [0, ft(length(ft)), f14, 0], 'y');
set(p2, 'LineStyle', 'none');
dt = [dt vec(i)];
ft = [ft f14];
plot(dt, ft, '-b'); % 最后绘制图形
axis([f e ymin ymax]);
pause(0.0001); % 短暂暂停,产生动画
end
end
这里有几个小细节。第一是,如果循环的时候不将 $t$ 和 $f_{14}$ 都添加到一个向量中,而直接使用 plot 函数的话,会发生只能画散点图的情况,画出来的图像不连续:
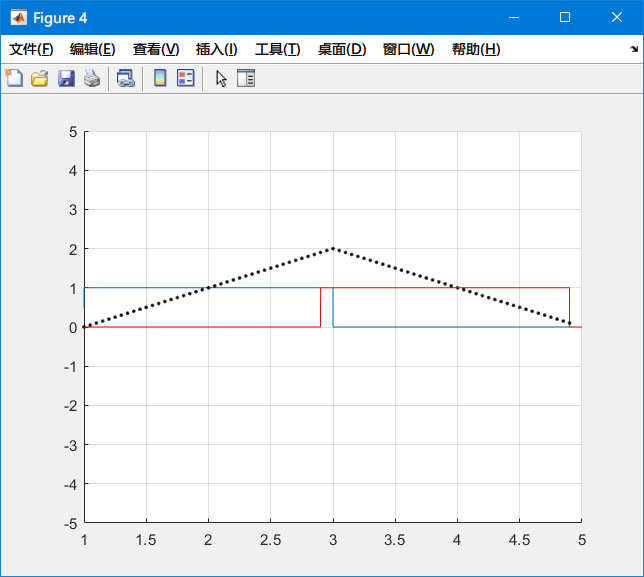
因此每次循环都将 $t$ 和 $f_{14}$ 加到已经计算过的向量 $dt$ 和 $ft$ 中,再次调用 plot 函数就能绘出光滑的直线/曲线:
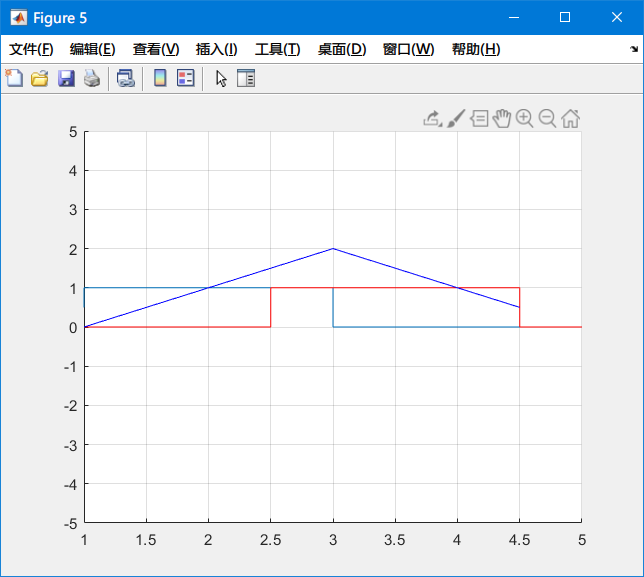
还有就是将卷积曲线下半部分填充的方式,MATLAB 可以用 fill([x_coordinate], [y_coordinate], color) 来填充一个多边形,根据简单的几何知识,我们只要填充一个小梯形即可:
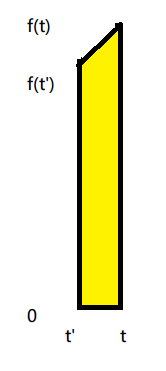
OK,现在让我们拿两个任意函数来卷积一下,看看效果如何。不如我们令 $f_1(t) = \frac{1}{2}t[u(t)-u(t-2)], f_2(t) = (1-\frac{|t|}{2})[u(t+2)-u(t-2)]$ ,演示一下 $f_1 * f_2$ 吧:
syms t;
f1 = 1/2 * t * (heaviside(t) - heaviside(t - 2));
f2 = (1 - 1/2 * (abs(t))) * (heaviside(t + 2) - heaviside(t - 2));
d = 0.1;
t1 = 0 : d : 2;
t2 = -2 : d : 2;
convolution_example(f1, f2, t1, t2, d);
效果图:
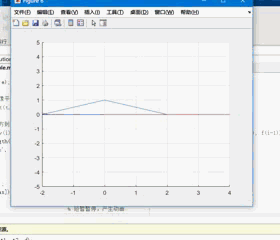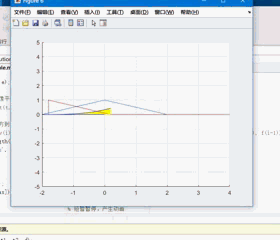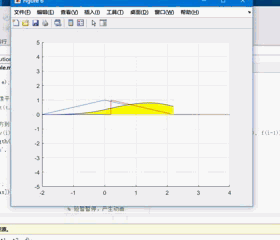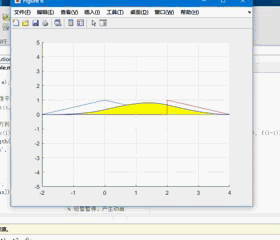
对比一下我们用普通连续信号卷积函数计算出来的结果图:
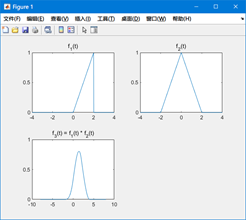
似乎挺不错。一个多小时的折腾似乎没白干。
那么问题来了,我为什么不直接去网上 Ctrl+C Ctrl+V 一份别人写好的呢?
别问,问就是吃饱撑着。
