emmm… FCS2017 夏令营的一道题目……用的是分治的算法，为了题目的一些细节本蒟蒻足足推了两个小时QAQ……所以要写篇文章记录一下不然哪天自己就看不明白了……

由于我比较啰嗦，以及我太弱了导致文章有可能有一些部分讲错了，所以，大家将就着看一下吧（虽然我不相信有人看）。

奇怪的道路

问题描述

从前，有一座网格城市，城市中每个房子占据一个正方形小格子的中 心，每个正方形小格子的边长均为1。

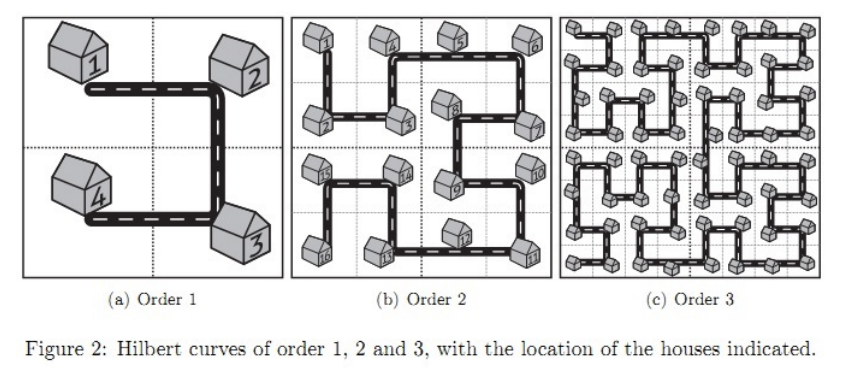
这座城市道路的设计方式是这样的，首先，定义(𝑎)图为一个基本图形，其阶为1，之后，将(𝑎)图中每一个房子都用一个基本图形代替，得到(𝑏)图，那么(𝑏)图的阶即为2，再将(𝑏)图中的每一个房子都用基本图形替代，得到阶为3的©图，以此类推，只要知道这座城市的阶𝑛，就可以知道它的道路设计。

这种七拐八弯的道路设计使得这座城市之间的道路交通运输相当不便，于是该市的市长决定改造一下这座城市的道路，但在此之前他需要做一系列的评估，比如这座网格城市中，连接第𝑖1行第𝑗1列的房屋与第𝑖2行第𝑗2列的房屋之间（两座房屋可能相同）的道路有多长，由于这种道路设计太过奇怪，人力难以计算，于是这个任务就交给作为软件工程师的你了。

输入格式

每个测试点第一行有两个正整数𝑛, 𝑇，表示城市的阶数和询问数。 接下来𝑇行，每行4个正整数𝑖1 𝑗1 𝑖2 𝑗2，表示要查询的两个房屋的坐标。

输出格式

对每个询问输出一行相应的值表示答案。

样例输入

2 4 2 1 3 1 3 2 2 2 2 3 3 3 3 4 2 4

样例输出

13 11 1 3

样例解释

样例对应题目中的(𝑏)图。 第一个询问问的是图中编号为2的房子与编号为15的房子的距离。 第二个询问问的是图中编号为14的房子与编号为3的房子的距离。 第三个询问问的是图中编号为8的房子与编号为9的房子的距离。 第四个询问问的是图中编号为10的房子与编号为7的房子的距离。

数据规模

Easy：对于30%的数据，1 ≤ 𝑛 ≤ 3。 Normal：对于60%的数据，1 ≤ 𝑛 ≤ 8。 Hard：对于100%的数据，均有1 ≤ 𝑛 ≤ 15，1 ≤ 𝑖1, 𝑗1, 𝑖2, 𝑗2 ≤ 2𝑛，1 ≤ 𝑇 ≤ 10000。

思路

观察题意，不难看出，对于给定的坐标 (x1, y1) 和 (x2, y2)，记他们所对应的房子编号分别为 A, B，要求 A, B 两个房子之间的距离，可以看出这个距离等于编号A - 编号B 的绝对值，记这个距离为 x，则我们可以看出：x = abs(A - B)。既然距离是由两个房子的编号唯一决定，那么我们就可以将目标转移到求这两个坐标对应的房子的编号上。

首先看 n 的范围不超过 15，也就是说最大的房子数量不超过 4 ^ 15 = 1073741824，做预处理的话开不下这么大的空间。这启示我们，一定存在一种方法，对于给定的一个城市坐标 (x, y)，通过这种方法能够直接推算出这个坐标所对应的房子编号。

我们先观察这个图：观察当 n >= 2 时候的图形，可以发现图形有这样的规律：基本图形总是会占满整个四分之一矩阵后，才会进入下一个四分之一矩阵。通过这样的规律，我们又能发现这四个被均分的矩阵具有相似的子结构，所以我们可以想到——分！治！

接下来，目标转移到找到这个方法。题意告诉我们，对于任意已知的 n，以从上到下（行）为 x 轴正方向，以从左到右（列）为 y 轴正方向，第一个房子的坐标一定位于 (1, 1)，第 4^n 个房子一定位于 (2^n+1, 1)，所以根据这个性质我们一定能够推算出这个城市的具体道路规划图。

问题在于，编号和坐标之间有没有什么关系？当然这种琢磨不透的题目一定不会让你一眼看出这个关系，所以我们需要一点小小的计算：

首先让我们看当 n = 1，即这个城市只有 1 阶，边长为 2^1=2，房子数 4^1 = 4。根据题意，我们有这样的关系：

  1     2
=========
1 1 --- 2
        |
        |
        |
2 4 --- 3

可以看到对于这样的矩阵，知道坐标的区间，就可以唯一确定城市的房子了。比如说在这里，(1, 1) 就对应房子 1。至于为什么和怎么确定，我们下面再说。不过说到这里有人还是会对这个 flag 将信将疑：坐标对应的房子可能会受到这个“基本图形”开口的影响，凭什么说它可以唯一确定一个房子的编号？的确，假如它的开口不同，就会导致这个性质是错的。既然如此我们就把这个反例消灭，保证一个子矩阵始终满足这个基本图形的性质。具体地说，对于已知 n = k 的 k 阶矩阵，一定要满足这个性质：

在最左上方取到这个矩阵中数的最小值，并在最左下方取到这个矩阵中数的最大值。

具体的操作，比如说我们看下面的这个图，这也是由基本图形变形而来的：

 1     4
 |     |
 |     |
 2 --- 3

那么怎么把它变成基本图形那样，可能大家的第一想法是旋转。但是旋转之后，并不满足在左上取最小值和左下取最大值的性质，所以旋转是不行的。所以我们采取另外一个方法，就是对称。例如上图中，我们取 1, 3 连接而成的对角线为对称轴，将这个图形沿着轴对称，那么这个图形就在还原回基本图形的同时，也保持了这个性质。

现在又有一个问题。如何知道什么时候对称，沿什么轴来对称？根据分治的思想我们再观察四个图形，我们发现，记当 n=k 的时候边长为 E, 则 E = 2^k，节点数为 N, 则 N = 4^k. 以中点为界将这个矩阵划分为相等的四个部分，右上角的矩阵和右下角的矩阵会始终保持着这个性质，那么我们的对称操作只需要对左上和左下的两个矩阵执行就可以了。观察左上和左下的两个矩阵，我们在确定对称轴的时候只需要找到对称后还原出基本图形及满足其性质（窝说话太啰嗦了，所以希望你们还记得这个性质）的那一条对称轴即可。再看图形，我们很容易找出，使得左上部分矩阵符合以上性质的对称轴为从左上到原矩阵中心位置的这条对角线，同样我们为左下矩阵找到的对称轴为从左下到原矩阵中心位置的这条对角线。

下面开始用坐标推算房子的编号。我们规定getnum(n, x, y)为第 n 阶中坐标位于 (x, y) 的房子的编号，并且规定当 n = 0 的时候，getnum(0, 1, 1) = 1。令 edgeMid = 当前阶的大矩阵边长的一半，有 mid = 2^(n-1)，nodeNum = 当前阶的大矩阵被四均分后的节点数目，有 node = 4^(n-1) = 2^(2n-2).

注意到我们刚才提到的性质1：基本图形会先填满一个四分之一矩阵之后，才会进入下一个矩阵。而且无论 n 为何值，进入四个矩阵的先后顺序一定是：左上 => 右上 => 右下 => 左下。所以呢，对于右上的矩阵，编号最小的房子一定是 nodeNum + 1；对于右下的矩阵，编号最小的房子一定是 2 × nodeNum + 1；对于左下的矩阵，编号最小的房子一定是 3 × nodeNum + 1。最大的也很容易推出。

先从简单的两个子矩阵——也就是不需要做任何对称的两个矩阵入手：对于每个阶段右上和右下这两个不需要做对称操作的部分，其坐标和编号的关系是显然的一个递推式：

// 右上
index = 1 * nodeNum + getnum(n - 1, x, y - edgeMid);

// 右下
index = 2 * nodeNum + getnum(n - 1, x - edgeMid, y - edgeMid);

其中进行坐标变换是为了确保起点为 (1, 1)，终点为 (2^n+1, 1)，这样根据坐标推出的编号才会成立。

进行对称操作的部分的坐标需要进行额外的小变化，因为进行了对称，所以我们要将 x 和 y 进行反转。同样也要进行坐标变换确保起点为 (1, 1) 和 (2^n+1, 1)。这里要注意一下左下矩阵的边界处理。

// 左上
index = getnum(n - 1, y, x);

// 左下
index = 3 * nodeNum + getnum(n - 1, edgeMid + 1 - y, 2 * edgeMid + 1 - x);

注意这里的坐标轴方向是以向下为 x 轴正方向，向右为 x 轴负方向，这样大家画一画草图就可以很容易地推出左下矩阵这个让人看了十分害怕的递推式。

至此，我们的目的——根据节点坐标推算它的编号——已经达到了。不信的话你可以随便找个点按照上面的递推式试一下。

以下贴的是参考代码。事实上理解了上面的内容，代码也就不难出来了。

示例代码 (C++)

#include <bits/stdc++.h> 
int getNum(int stage, int x, int y)
{
  if (stage == 1) {
    if (x == 1 && y == 1)
      return 1;
    if (x == 1 && y == 2)
      return 2;
    if (x == 2 && y == 2)
      return 3;
    if (x == 2 && y == 1)
      return 4;
  }
  
  int edgeMid = 1 << (stage - 1),					// edgeMid = 2^(stage-1)
      nodeNum = 1 << (2 * (stage - 1));   // nodeNum = 4^(stage-1) = 2^2(stage-1)
  
  if (x <= edgeMid && y <= edgeMid)
    return getNum(stage - 1, y, x);
  if (x <= edgeMid && y > edgeMid)
    return nodeNum + getNum(stage - 1, x, y - edgeMid);
  if (x > edgeMid && y > edgeMid)
    return 2 * nodeNum + getNum(stage - 1, x - edgeMid, y - edgeMid);
  if (x > edgeMid && y <= edgeMid)
    return 3 * nodeNum + getNum(stage - 1, edgeMid + 1 - y, 2 * edgeMid + 1 - x);
  
}

int main()
{
  freopen("road.in", "r", stdin);
  freopen("road.out", "w", stdout);
  
  int n, T;
  scanf("%d%d", &n, &T);
  
  while (T--)
  {
    int x1, y1, x2, y2;
    scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
    printf("%d\n", abs(getNum(n, x1, y1) - getNum(n, x2, y2)));
  }
  
  fclose(stdin);
  fclose(stdout);
  
  return 0;
}

这样我们就圆满地解决了这个问题。 —— 题解

• 原题版权归出题人所有。